در یک صحنه نبرد شطرنج، موقعیتی برای سفید فراهم آمده که می تواند او را برنده قاطع این بازی نماید.
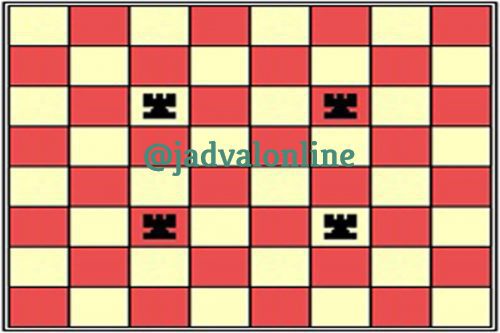
در یک صفحه شطرنج، ۴ رخ همانند آنچه در بالا می بینید، چیده شده اند. آیا می توانید بگویید چه تعداد مربع (با هر اندازه ای) قابل شمارش هستند که در آنها رخی وجود نداشته باشد؟
.
.
.
.
.
.
.
.
.
.
.
پاسخ معما
۹۳ مربع قابل شمارش است: توضیح:باید تعداد مربع های این صفحه شطرنج، از مربع های ۱×۱ به بالا که شامل مهره رخ نیستند را بشماریم، به این ترتیب خواهیم داشت: مربع های ۱×۱: ۶۰ مربع (۴-۶۴) مربع های ۲×۲: ۳۳ مربع (۱۶-۴۹) هیچ مربعی با اندازه ۳×۳ و بالاتر نمی توانیم پیدا کنیم که شامل رخ نباشد. پس در مجموع ۹۳ مربع قابل شمارش خواهند بود.